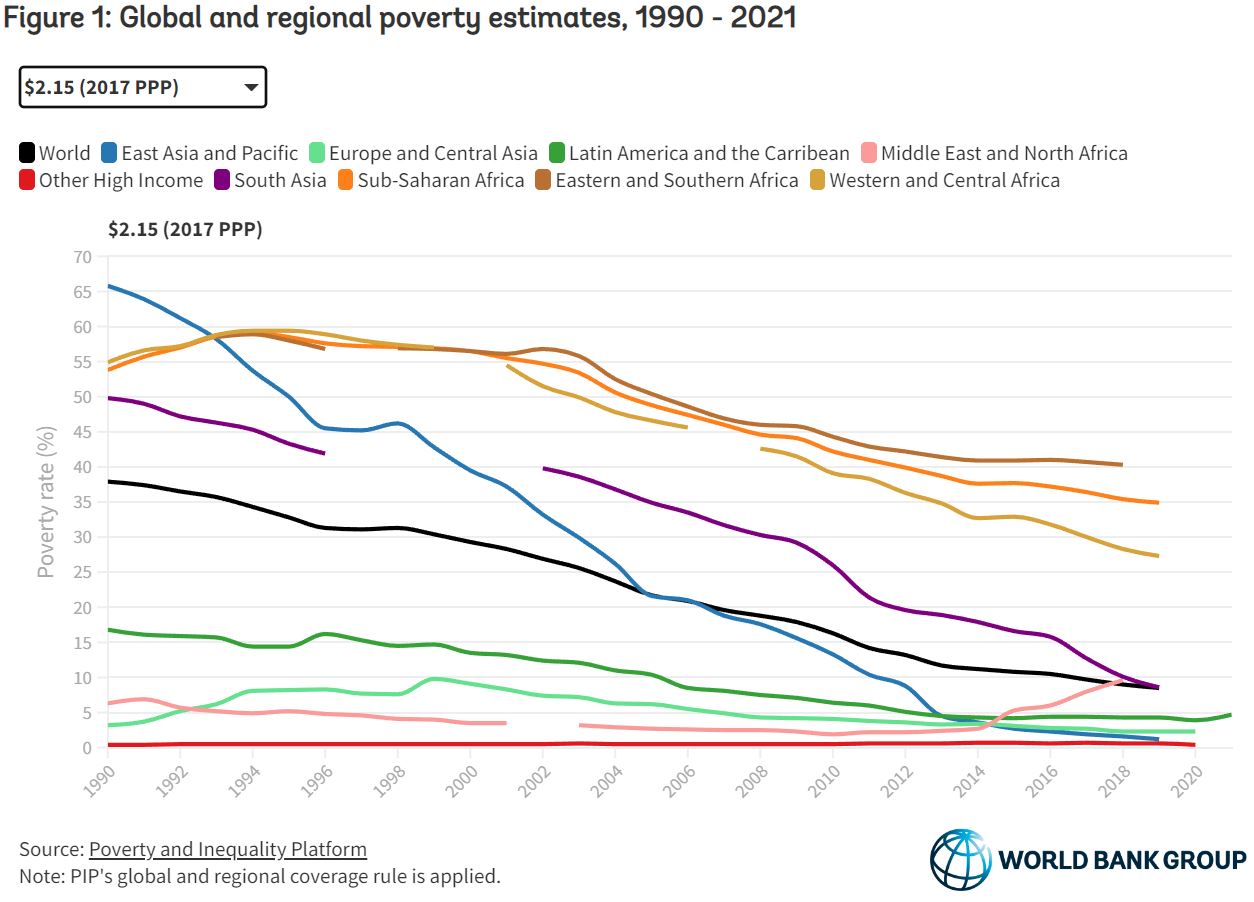
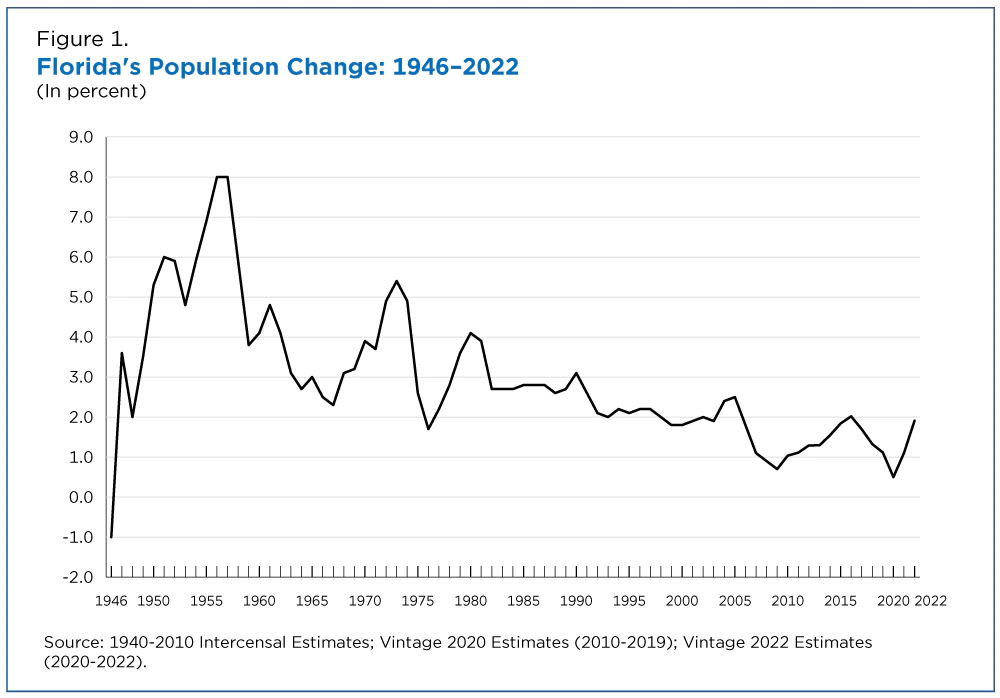
You probably looked at the graph already and know the answer, Florida. The graph is from the Census Bureau article New Florida Estimates Show Nation’s Third-Largest State Reaching Historic Milestone by Marc Perry, Luke Rogers and Kristie Wilder (12/22/2022). This leaves us with more questions than answers, which we’ll get to. First,
You probably looked at the graph already and know the answer, Florida. The graph is from the Census Bureau article New Florida Estimates Show Nation’s Third-Largest State Reaching Historic Milestone by Marc Perry, Luke Rogers and Kristie Wilder (12/22/2022). This leaves us with more questions than answers, which we’ll get to. First,
After decades of rapid population increase, Florida now is the nation’s fastest-growing state for the first time since 1957, according to the U.S. Census Bureau’s Vintage 2022 population estimates released today.
Florida’s population increased by 1.9% to 22,244,823 between 2021 and 2022, surpassing Idaho, the previous year’s fastest-growing state.
Florida wins by percent but did Florida add the most population?
Increasing by 470,708 people since July 2021, Texas was the largest-gaining state in the nation, reaching a total population of 30,029,572. By crossing the 30-million-population threshold this past year, Texas joins California as the only states with a resident population above 30 million. Growth in Texas last year was fueled by gains from all three components: net domestic migration (230,961), net international migration (118,614), and natural increase (118,159).
Florida was the fastest-growing state in 2022, with an annual population increase of 1.9%, resulting in a total resident population of 22,244,823.
If Florida grew by 1.9% and was the fastest, what was the U.S. growth?
After a historically low rate of change between 2020 and 2021, the U.S. resident population increased by 0.4%, or 1,256,003, to 333,287,557 in 2022, according to the U.S. Census Bureau’s Vintage 2022 national and state population estimates and components of change released today.
The last two quotes are from the Census Bureau press release Growth in U.S. Population Shows Early Indication of Recovery Amid COVID-19 Pandemic (12/22/2022). Plenty of QL uses for these articles and you can follow the link in the last quote for data.
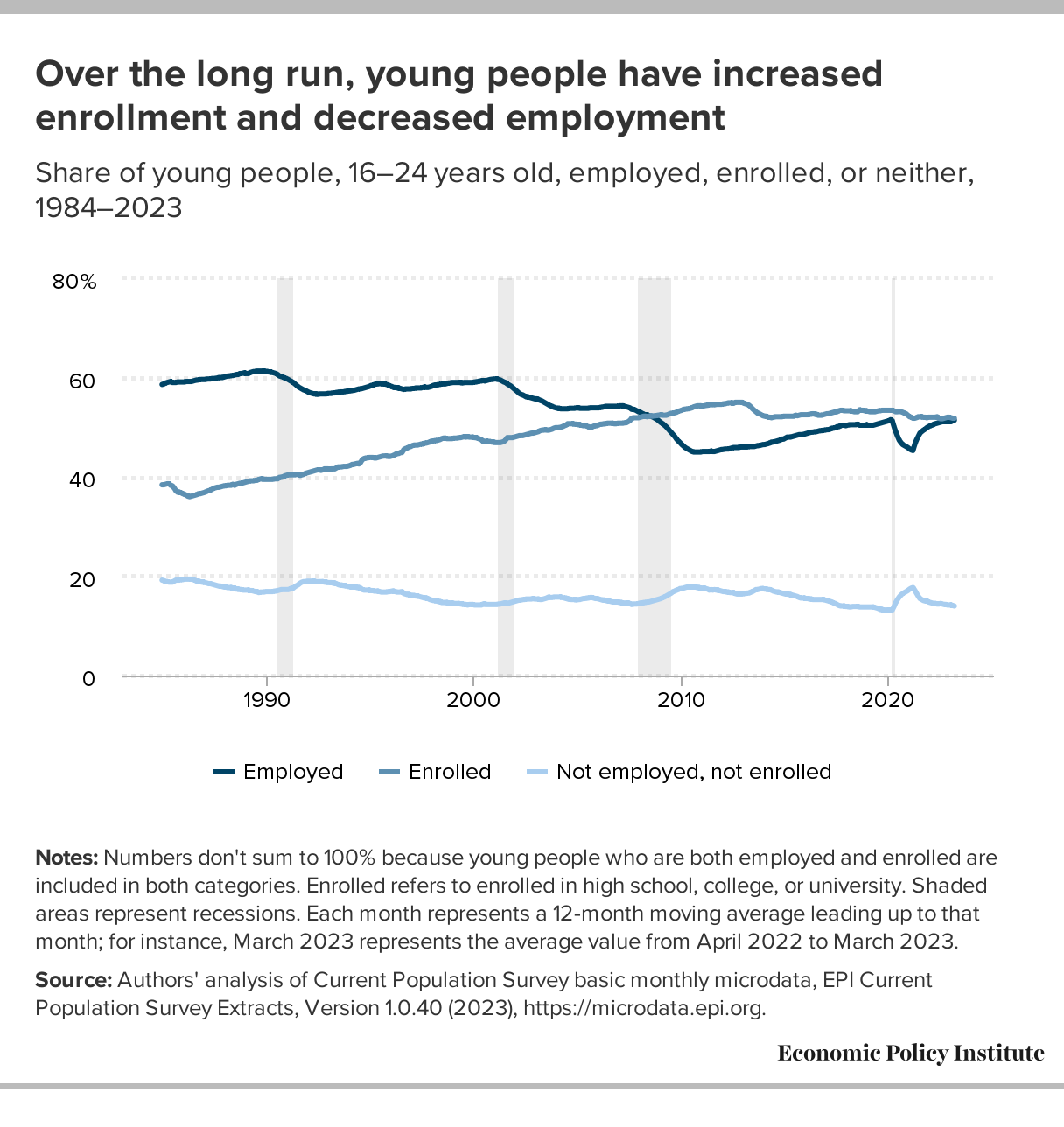 The graph here is from the EPI article Class of 2023: Young adults are graduating into a strong labor market by Elise Gould, Jori Kandra, and Katehrine deCourcy (5/3/2023). They note:
The graph here is from the EPI article Class of 2023: Young adults are graduating into a strong labor market by Elise Gould, Jori Kandra, and Katehrine deCourcy (5/3/2023). They note: